Exponencial periódica compleja
Transformación de la variable independiente

Papito no nació para las ocho horas
Sin duda uno de los mejores descubrimientos del 2013 fue Cuarteto de Nos. Una combinación extraordinaria de rima, humor, sarcasmo y realismo hacen de muchas de las canciones de este grupo uruguayo verdaderas joyas de la música. Y una de ellas, Pobre Papá, me dejó pensando en las ocho horas de trabajo diario. Así que un día usé el fenomenal Python y línea tras línea conseguí un código que marca el horario de salida del trabajo.
Este sencillo código lo he venido usando ya bastante tiempo. Le doy F5 todos los días.
Leyendo el extraordinario libro Abre tu mente a los números de la Dra. Barbara Oakley descubrí una idea interesante: el trabajo duro combinado con un ocio saludable es una combinación que mejora nuestra productividad en los estudios (o el trabajo).
Así que aquí está: saber la hora exacta de salida de esas ocho horas que se aprovecharon usando el modo concentrado y el modo difuso...
hora_ent_m =7
minuto_ent_m =32
hora_sal_m =12
minuto_sal_m =44
hora_ent_t =14
minuto_ent_t =33
print(str(hora_ent_m)+':'+str(minuto_ent_m))
print(str(hora_sal_m)+':'+str(minuto_sal_m))
print(str(hora_ent_t)+':'+str(minuto_ent_t))
hora_m=hora_sal_m-hora_ent_m;
minu_m=minuto_sal_m-minuto_ent_m;
if minu_m<0:
hora_m=hora_m-1;
minu_m=60+minu_m;
print('-'*40)
print('Horas manana: '+str(hora_m)+':'+str(minu_m))
#Restan
rth=7-hora_m
rtm=60-minu_m
if rtm>=60:
rtm=00;
rth=rth+1
if rtm<10:
print('Horas restantes: '+str(rth)+':0'+str(rtm))
else:
print('Horas restantes: '+str(rth)+':'+str(rtm))
#Salida
hora_salida=hora_ent_t+rth
minuto_salida=minuto_ent_t+rtm
if minuto_salida>=60:
minuto_salida=minuto_salida-60
hora_salida=hora_salida+1
if minuto_salida<10:
print('Hora de salida: '+str(hora_salida)+':0'+str(minuto_salida))
else:
print('Hora de salida: '+str(hora_salida)+':'+str(minuto_salida))
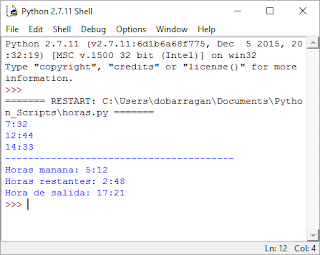
Aquí el resultado:
Captura de vídeo en GUI Matlab
function video_gui_OpeningFcn(hObject, eventdata, handles, varargin) movegui(hObject,'center') set(handles.axes1,'XTick',[ ],'YTick',[ ]) set(handles.axes2,'XTick',[ ],'YTick',[ ]) imaqreset handles.output = hObject; guidata(hObject, handles);Con la herramienta Object browser podemos ver el campo tag de cada elemento de la GUI. (Ver Figura siguiente). El botón de inicio de la GUI abre un programa que de forma automática detecta las cámaras de vídeo (Ver Figura siguiente). En la función de apertura contiene el código del Listado siguiente.
function sel_camera_OpeningFcn(hObject, eventdata, handles, varargin)
imaqreset;
set(handles.ok_b,'Enable','off')
hw=imaqhwinfo('winvideo');
handles.cam=hw;
set(handles.lista_camaras,'String',{hw.DeviceInfo.DeviceName})
handles.output = hObject;
guidata(hObject, handles);
Con el pop up menu seleccionamos qué cámara usar. Dentro de la función asociada a este elemento (mostrada en el Listado siguiente) está la programación que extrae las principales características de la cámara seleccionada.
function lista_camaras_Callback(hObject, eventdata, handles)
pos=get(handles.lista_camaras,'Value');
hw=handles.cam;
id=hw.DeviceIDs{pos};
set(handles.id_camara,'String',id)
formatos=hw.DeviceInfo(pos).SupportedFormats;
set(handles.formatos,'String',formatos)
list_f = [formatos{1:end}];
si=strfind(list_f,'RGB24_320x240');
if isempty(si)
es_web_ext=0;% Laptop: YUY2
else
es_web_ext=1;% External: RGB
end
handles.es_web_ext=es_web_ext;
handles.id=id;
guidata(hObject, handles)
set(handles.ok_b,'Enable','on')
Al presionar el botón Ok se exportan las características de la cámara seleccionada. El Listado siguiente contiene el código de la función del botón. Note que se usan variables globales para exportar esta información a la primera GUI.
function ok_b_Callback(hObject, eventdata, handles) global id es_web_ext es_web_ext = handles.es_web_ext; id = handles.id; close (handles.camara)Regresando a la programación del la primera GUI, una vez seleccionada la fuente de vídeo, el botón de inicio muestra la secuencia de imágenes en el primer axes de la GUI (Ver Listado siguiente).
function inicio_b_Callback(hObject, eventdata, handles) set(handles.inicio_b,'Enable','off') start(handles.vidobj); vidRes = get(handles.vidobj,'VideoResolution'); nBands = get(handles.vidobj,'NumberOfBands'); hImage = image(zeros(vidRes(2), vidRes(1), nBands),'Parent',handles.axes1); preview(handles.vidobj,hImage); guidata(hObject, handles);Con el botón de captura, cuya programación se muestra en el Listado siguiente, obtenemos la imagen a partir del vídeo.
function captura_Callback(hObject, eventdata, handles)
try
rgb = getsnapshot(handles.vidobj);
if handles.es_web_ext==0
rgb = ycbcr2rgb(rgb);
end
image(rgb,'Parent',handles.axes2);
axes(handles.axes2)
axis off
catch
disp('No hay imagen para mostrar')
end
Finalmente, el botón de parada detiene la proyección de vídeo y permitirá seleccionar una nueva fuente de vídeo. (Ver Listado siguiente.)
function parar_b_Callback(hObject, eventdata, handles) set(handles.inicio_b,'Enable','on') stoppreview(handles.vidobj)
GUI de Matlab para encontrar el punto de corte de dos funciones.
% --- Executes just before corte_graficas is made visible. function corte_graficas_OpeningFcn(hObject, eventdata, handles, varargin) set(handles.pushbutton2,'Enable','off') handles.output = hObject; guidata(hObject, handles);El código que se ejecuta el presionar el primer botón se muestra a continuación. Se generan dos funciones y se colocan sus valores en handles para poder exportar estos valores a otra función del archivo .m.
% --- Executes on button press in pushbutton1. function pushbutton1_Callback(hObject, eventdata, handles) x = 0:0.01:10; y1 = x .^2 + 2; y2 = x .^3 ; handles.x=x; handles.y1=y1; handles.y2=y2; handles.axes1; plot(x, y1, x, y2); ylim([0,10]) set(handles.pushbutton2,'Enable','on') guidata(hObject, handles);Finalmente, el botón etiquetado como Corte ejecuta el código que encuentra el punto de corte de las dos gráficas y presenta la coordenada en el cuadro estático de texto.
% --- Executes on button press in pushbutton2. function pushbutton2_Callback(hObject, eventdata, handles) idx = find(handles.y1 - handles.y2 < eps, 1); %// Index of coordinate in array px = handles.x(idx); py = handles.y1(idx); set(handles.text1,'String',['x= ',num2str(px),' y= ',num2str(py)]) handles.axes1; hold on plot(px, py, 'ro', 'MarkerSize', 18) hold off
Cosenoidal con varias fases en Matlab.
t=-1:1/100:1;
cc=['r','g','b'];
w0=2*pi;
desv_tmp=zeros(1,3);
for k=1:3
theta=[-pi/2,-pi,-1.5*pi];
desv_tmp(k)=theta(k)/w0;
z=8*cos(2*pi*t + theta(k));
plot(t,z,'LineWidth',2,'Color',cc(k))
hold on
grid on
end
hold off
Gráfica del seno y coseno con la identidad de Euler en Matlab.
t=-1:1/100:1; s1=2*cos(4*pi*t); s2=2*sin(4*pi*t); subplot(2,1,1) plot(t,s1,'LineWidth',2),grid on subplot(2,1,2) plot(t,s2,'LineWidth',2),grid on